Statistics Chapter 18 Review a 2012 Pearson Education Inc Answers

Chapter xviii Confidence Intervals for Proportions Copyright © 2015, 2010, 2007 Pearson Instruction, Inc. Chapter 18, Slide one -1 1

Standard Error n Nosotros learned that the sampling distribution of proportions has a standard deviation: Copyright © 2015, 2010, 2007 Pearson Education, Inc. Affiliate 18, Slide 1 -ii two

Standard Mistake (cont. ) n n n When we don't know p, we're stuck, right? Nope. We will use sample statistics to estimate these population parameters. Whenever nosotros guess the standard difference of a sampling distribution, nosotros call it a standard mistake. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter eighteen, Slide i -3 three

Standard Fault (cont. ) n For a sample proportion, the standard error is Copyright © 2015, 2010, 2007 Pearson Instruction, Inc. Chapter eighteen, Slide 1 -4 4

A Confidence Interval n Recall that the sampling distribution model of centered at p, with standard deviation northward is . Since we don't know p, nosotros can't observe the true standard deviation of the sampling distribution model, and then we need to find the standard fault: Copyright © 2015, 2010, 2007 Pearson Education, Inc. Affiliate 18, Slide ane -half dozen half-dozen

A Confidence Interval (cont. ) n n By the 68 -95 -99. seven% Rule, we know northward about 68% of all samples volition have 's within i SE of p n about 95% of all samples will take 'south within 2 SEs of p due north most 99. 7% of all samples will have 'due south within 3 SEs of p We can look at this from 's signal of view… Copyright © 2015, 2010, 2007 Pearson Pedagogy, Inc. Chapter 18, Slide ane -seven 7

A Confidence Interval (cont. ) due north due north Consider the 95% level: due north If we reach out ii SEs, nosotros are 95% sure that p will exist in that interval. In other words, if we accomplish out 2 SEs in either direction of , we tin can exist 95% confident that this interval contains the true proportion. This is called a 95% conviction interval. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter xviii, Slide 1 -8 eight

A Confidence Interval (cont. ) Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter eighteen, Slide 1 -nine nine

What Does " 95% Confidence" Really Hateful? n due north Each confidence interval uses a sample statistic to estimate a population parameter. But, since samples vary, the statistics we employ, and thus the conviction intervals nosotros construct, vary as well. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Affiliate 18, Slide one -ten 10

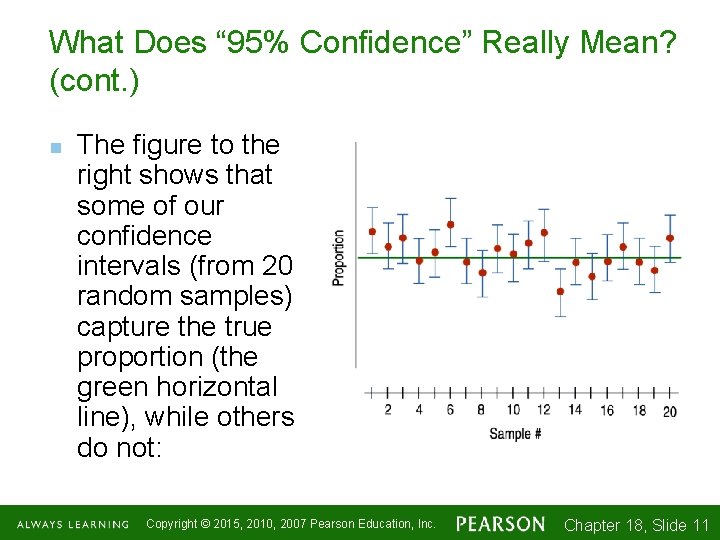
What Does " 95% Conviction" Really Mean? (cont. ) n The effigy to the right shows that some of our confidence intervals (from twenty random samples) capture the true proportion (the dark-green horizontal line), while others do non: Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide 1 -11 11

What Does " 95% Confidence" Really Hateful? (cont. ) n due north Our conviction is in the process of amalgam the interval, not in any 1 interval itself. Thus, we look 95% of all 95% confidence intervals to contain the truthful parameter that they are estimating. Copyright © 2015, 2010, 2007 Pearson Instruction, Inc. Affiliate 18, Slide one -12 12

Margin of Error: Certainty vs. Precision n We tin claim, with 95% confidence, that the interval contains the truthful population proportion. n The extent of the interval on either side of is called the margin of fault (ME). In general, confidence intervals have the form estimate ± ME. The more confident we want to be, the larger our ME needs to be, making the interval wider. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide 1 -xiii 13

Margin of Mistake: Certainty vs. Precision (cont. ) Copyright © 2015, 2010, 2007 Pearson Teaching, Inc. Chapter eighteen, Slide one -14 xiv

Margin of Error: Certainty vs. Precision (cont. ) n n n To be more confident, we wind up existence less precise. n Nosotros demand more values in our conviction interval to be more sure. Because of this, every confidence interval is a rest between certainty and precision. The tension between certainty and precision is always there. n Fortunately, in most cases nosotros can be both sufficiently certain and sufficiently precise to make useful statements. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Affiliate 18, Slide i -15 15

Margin of Error: Certainty vs. Precision (cont. ) n n The pick of confidence level is somewhat capricious, merely keep in heed this tension between certainty and precision when selecting your confidence level. The most unremarkably chosen conviction levels are ninety%, 95%, and 99% (but any percentage can exist used). Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter xviii, Slide i -16 16

Critical Values n n northward The ' 2' in (our 95% confidence interval) came from the 68 -95 -99. 7% Rule. Using a table or engineering science, we discover that a more verbal value for our 95% confidence interval is 1. 96 instead of 2. n We phone call 1. 96 the critical value and denote it z*. For any conviction level, we can detect the corresponding critical value (the number of SEs that corresponds to our conviction interval level). Copyright © 2015, 2010, 2007 Pearson Instruction, Inc. Chapter 18, Slide one -17 17

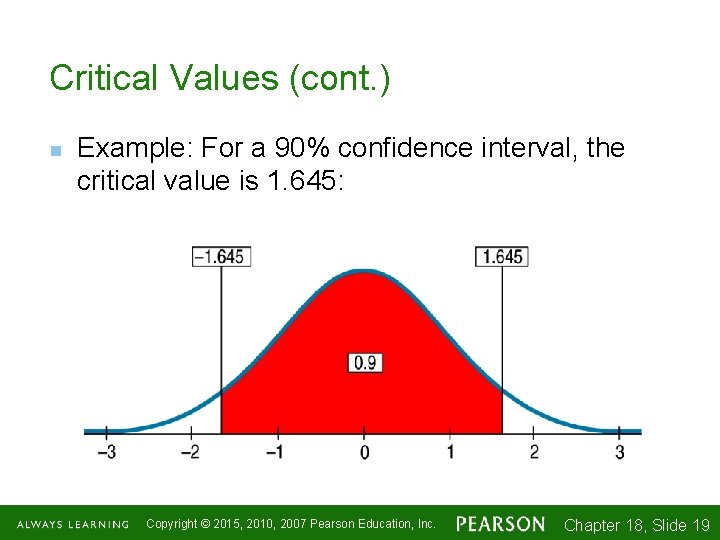
Critical Values (cont. ) northward Example: For a 90% confidence interval, the critical value is one. 645: Copyright © 2015, 2010, 2007 Pearson Education, Inc. Affiliate 18, Slide 1 -19 xix

Assumptions and Conditions n n All statistical models make upon assumptions. n Different models brand different assumptions. n If those assumptions are non truthful, the model might be inappropriate and our conclusions based on it may exist wrong. You can never be sure that an assumption is true, but yous tin often decide whether an assumption is plausible by checking a related condition. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide 1 -20 xx

Assumptions and Conditions (cont. ) n due north Here are the assumptions and the corresponding atmospheric condition you must bank check before creating a confidence interval for a proportion: Independence Assumption: We commencement demand to Retrieve about whether the Independence Assumption is plausible. It'south not one you tin can check past looking at the data. Instead, nosotros cheque two conditions to decide whether independence is reasonable. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide one -21 21

Assumptions and Weather condition (cont. ) Randomization Condition: Were the information sampled at random or generated from a properly randomized experiment? Proper randomization can help ensure independence. n 10% Status: Is the sample size no more than x% of the population? § Sample Size Supposition: The sample needs to exist large enough for us to exist able to use the CLT. due north Success/Failure Condition: We must expect at least ten "successes" and at to the lowest degree ten "failures. " n Copyright © 2015, 2010, 2007 Pearson Pedagogy, Inc. Affiliate 18, Slide 1 -22 22

One-Proportion z-Interval n n When the conditions are met, we are ready to find the conviction interval for the population proportion, p. The confidence interval is where n The critical value, z*, depends on the item conviction level, C, that y'all specify. Copyright © 2015, 2010, 2007 Pearson Pedagogy, Inc. Chapter 18, Slide 1 -23 23

Choosing Your Sample Size n n The question of how large a sample to take is an of import pace in planning whatsoever study. Cull a Margin or Error (ME) and a Confidence Interval Level. The formula requires which nosotros don't have still considering we have not taken the sample. A good estimate for , which will yield the largest value for (and therefore for n) is 0. 50. Solve the formula for n. Copyright © 2015, 2010, 2007 Pearson Teaching, Inc. Chapter 18, Slide i -24 24

What Can Go Incorrect? Don't Misstate What the Interval Means: due north Don't suggest that the parameter varies. n Don't claim that other samples will concur with yours. n Don't exist sure about the parameter. n Don't forget: It'southward nearly the parameter (not the statistic). n Don't claim to know also much. n Exercise take responsibility (for the dubiety). n Do care for the whole interval every bit. Copyright © 2015, 2010, 2007 Pearson Educational activity, Inc. Chapter 18, Slide 1 -26 26

What Tin Become Wrong? (cont. ) Margin of Error Also Large to Be Useful: n We tin't be exact, but how precise do we need to exist? due north 1 style to make the margin of error smaller is to reduce your level of conviction. (That may not exist a useful solution. ) n You need to think about your margin of error when y'all design your study. northward To get a narrower interval without giving upwardly confidence, you need to accept less variability. northward You can exercise this with a larger sample… Copyright © 2015, 2010, 2007 Pearson Pedagogy, Inc. Affiliate 18, Slide 1 -27 27

What Can Go Wrong? (cont. ) Choosing Your Sample Size: due north To be rubber, circular up the sample size yous obtain. And show your rounding as part of your work. Copyright © 2015, 2010, 2007 Pearson Pedagogy, Inc. Affiliate eighteen, Slide 1 -28 28

What Tin Go Wrong? (cont. ) Violations of Assumptions: northward Picket out for biased samples—keep in mind what you learned in Chapter 11. n Recall about independence. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide 1 -29 29

What take we learned? n north n Finally nosotros have learned to use a sample to say something about the world at large. This procedure (statistical inference) is based on our agreement of sampling models, and volition be our focus for the rest of the volume. In this chapter we learned how to construct a confidence interval for a population proportion. northward Best estimate of the true population proportion is the one we observed in the sample. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide ane -30 30

What take we learned? north n n n Best approximate of the true population proportion is the one we observed in the sample. Create our interval with a margin of error. Provides u.s.a. with a level of confidence. College level of confidence, wider our interval. Larger sample size, narrower our interval. Calculate sample size for desired degree of precision and level of confidence. Check assumptions and condition. Copyright © 2015, 2010, 2007 Pearson Didactics, Inc. Affiliate xviii, Slide 1 -31 31

What take we learned? n We've learned to interpret a confidence interval by Telling what we believe is truthful in the unabridged population from which nosotros took our random sample. Of class, we tin't be sure, but we can be confident. Copyright © 2015, 2010, 2007 Pearson Teaching, Inc. Chapter eighteen, Slide 1 -32 32

AP Tips due north northward Don't forget to check your weather condition. The AP test won't specifically ask you to, but it expects yous to do so. Ever. Be prepared to interpret the confidence level as a follow-up question to interpreting the interval. Copyright © 2015, 2010, 2007 Pearson Education, Inc. Chapter 18, Slide 1 -33 33

cookprinkin.blogspot.com

Source: https://slidetodoc.com/chapter-18-confidence-intervals-for-proportions-copyright-2015/

Share this post